
I. Abstract
The post-surgery face model construction is inspired by the doctors who want to improve the process of surgery. If they could know the real-time post-surgery model, it will be easy to discuss with the patients about the degrees of surgery they need. We got few pairs of pre-surgery and post-surgery pictures, whose purpose is shrinking the submaxillary and supramxillury. At the beginning, we simplify the entire processes into three major stages. First, we construct the 3D face models from 2D pictures and convert them into user-defined format, which can simplify the procedure. Second, align the pre-surgery and post-surgery models on the same coordinate. And then we can compute the difference between the pre-surgery and post-surgery models of each pairs. Collecting those variations to form the variation matrix, furthermore, applying PCA( Principal Component Analysis ) on this variation matrix. Therefore, we can get the main directions of variation by the surgery. In the last stage, we design a user interface to load a new patient¡¦s model, simulate the surgery and display the result. The following chart is the entire procedure of this project.
II. The Flow Chart

III. Implementation
IV. Experiment
VI. Conclusions and Suggestions
During the whole process, there may be some steps we can improve.
Since FaceGen Modeller only use three different sides look of photos, maybe it can¡¦t describe the change in surgery precisely. Furthermore, FaceGen Modeller use too few feature points to generate 3D model, so the unchanged part during the surgery in the model may vary too much result from model generating process.
2.The database¡¦s size is too small
Because of the variations cause by models generating( isn¡¦t cause by surgery) is unavoidable, we can omit them by ignore the eigenvectors those are correspond to small eigenvector. When the database isn¡¦t large enough, those variations will be included.
VI. Reference
1. Lindsay I Smith, ¡§A tutorial on Principal Components Analysis.¡¨ (2002)
2. Berthold K.P. Horn, ¡§Closed-form solution of absolute orientation using unit quaternions.¡¨ (1987)
3. Berthold K.P. Horn, Hugh M. Hilden, and Shahriar Negahdaripour, ¡§Closed-form solution of absolute orientation using orthonormal matrices.¡¨
4. http://en.wikipedia.org/wiki/Singular_value_decomposition
1. Construct 3D face models
(1.a) Use ¡§FaceGen Modeller¡¨ to generate face models
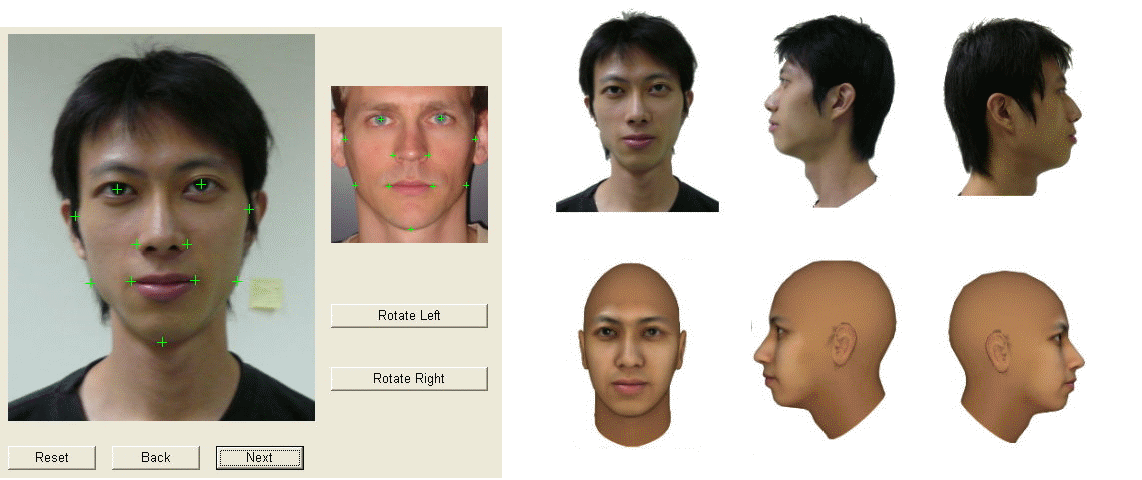
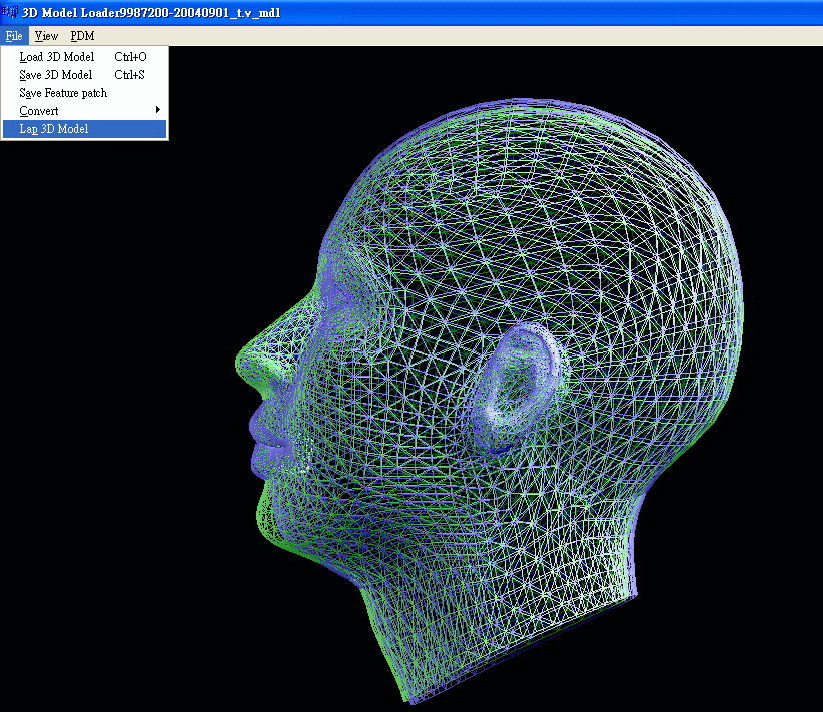
(1.b) Convert the output format (.3ds) into user-defined format
Because of the (.3ds) models those are generated in (1.a) step are inconvenient to handle, so that we want to convert them to the user-defined format(.v_mdl), which is including vertices (.v_vtx), polygons (.v_ply) and groups (.v_grp) information.
2. Compute the main directions of variation of the surgery
(2.a) Compute the absolute orientation between pre and post surgery models
To compute the absolute orientation between the pre and post surgery models, we may assume that parts of face areas aren¡¦t change during the surgery. We select some points in those areas to compute the absolute orientation.In our project,we assume that the vertices on cheeks and brow are consistent during the surgery.<\FONT>
(2.b) Apply the rotation, translation and scale matrices to pre-surgery model
By computing the absolute orientation, we get the rotation(R) and translation(T) matrices and scale(s) between the pre and post surgery model. Applying those matrice to the post-surjery model, we can align the two models on the same coordinate.
3. Learning the main variation of the surjery
We repeat the step2 to get all the variation vectors of the surgery. Integrate all the variation vectors together to form the variation matrix, each variation vector is one of column vector of the variation matrix. And then we apply PCA on this variation matrix. We get the main variation of the surgery.
Original pre-surjery model
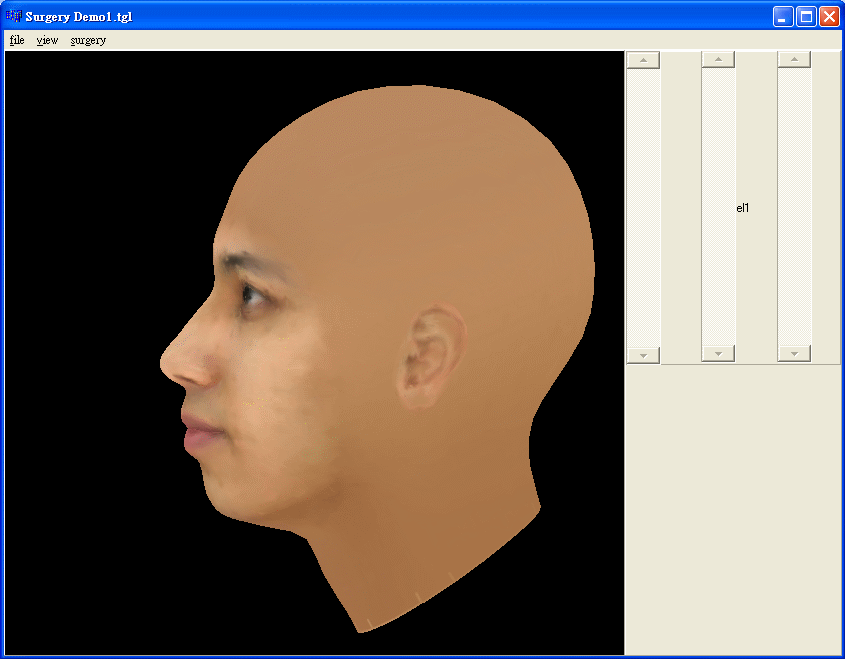
Applying the first eigenvector
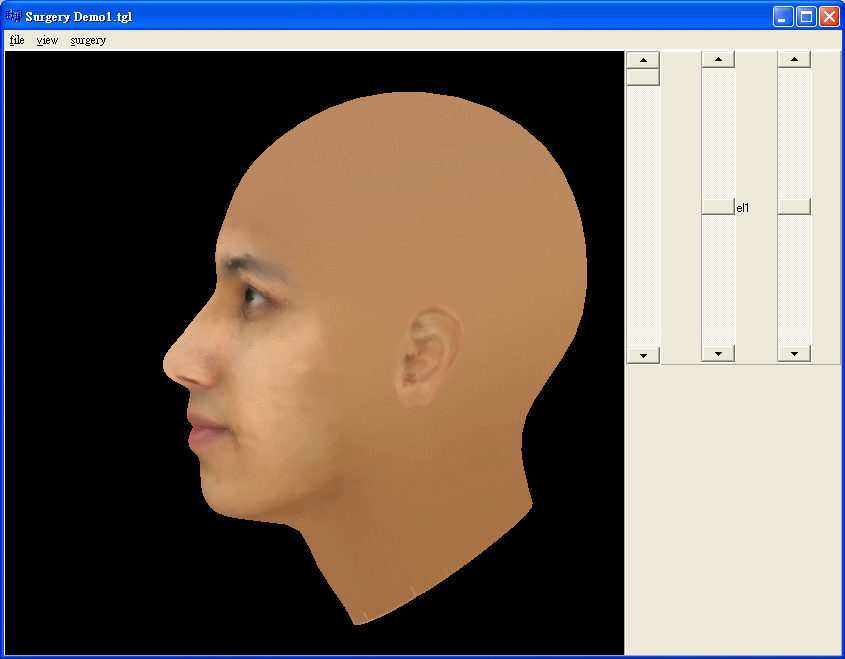
Applting the second eigenvector
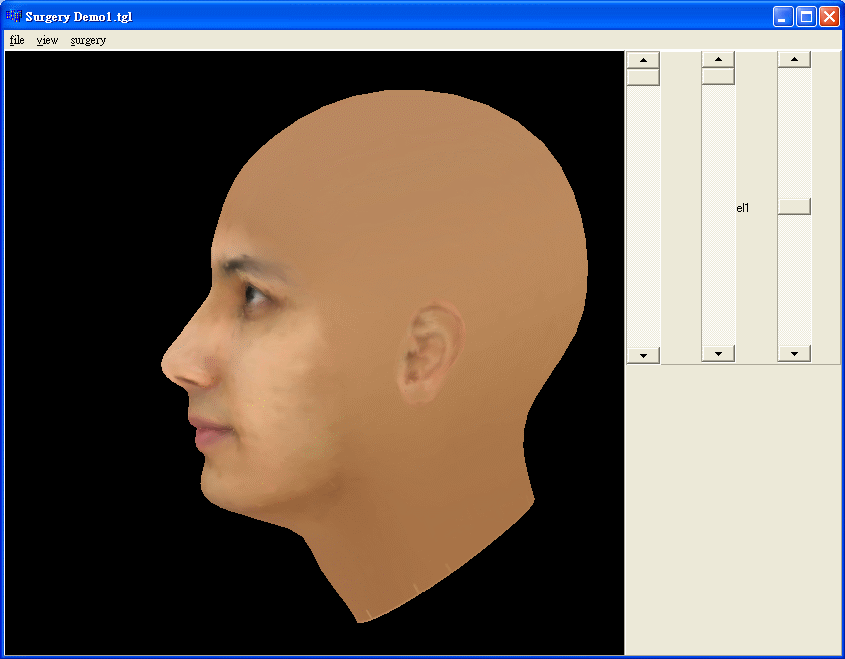
Applying the third eigenvector
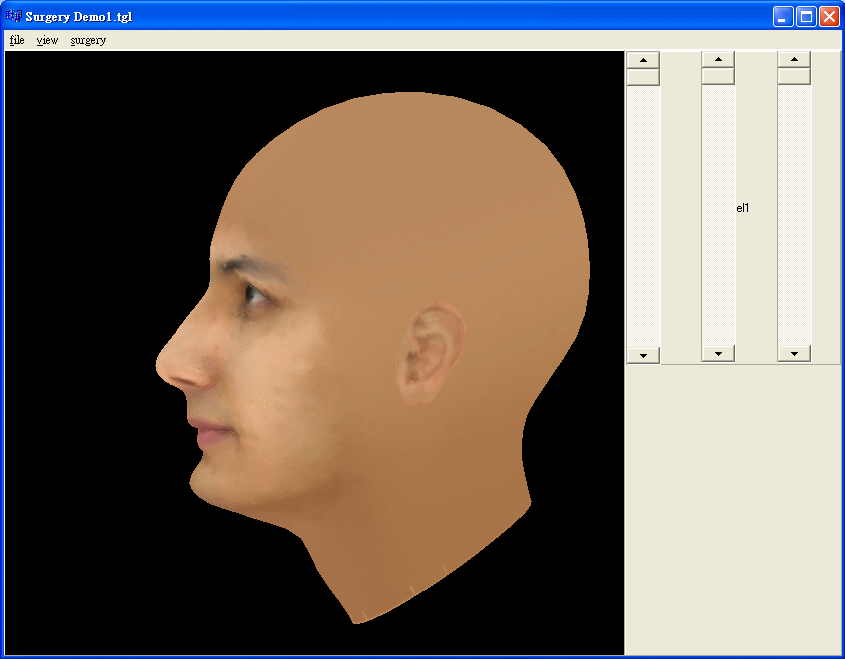
1.The modeling method