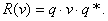Human Tracking and Motion Animation

指導教授：賴尚宏
姓名：吳奇峻、劉紹偉
學校：清華大學
系級：資工04級

1. Abstract

這一次專題，是研究如何模擬人體的運動。在模擬人體的運動中，有很多種的做法，例如「貼亮點」 就可以達成追蹤人體運動的目的。但是這次我們是利用DV拍一段影片，然後去追蹤人體的運動，再利 用網路上下載的人體模型，去模擬影片中人物的運動。

2. Our Approach

  • 模型處理

    1. 取得模型：根據老師所給的網址( http://www.cyberware.com/samples/ )，我們可以上網下載模型。
    2. 分析模型：上網下載的模型，我們可以利用Plyview軟體，去檢閱取得的模型，不論是大小，形狀都可以很清楚的顯示出來。
    3. 轉檔：利用Plyview可以把抓下來的模型轉成各式各樣的檔案模式，利如Visual Studio、object…等等。不過我們嘗試了取多檔案類型，後來決定用object file format，其檔案模式輸出的內容為：
      1. 所有點的數目以及所有點的資訊。
      2. 所有三角片對應的點。
    4. OpenGL：利用OpenGL來將取得點的資訊，顯示在電腦螢幕上，不過因為網上的模型跟我們OpenGL顯示的的座標軸有差異，因此我們修正取得的點而使模型是面向著我們。
    5. 截取部分資訊：因為人體的運動是根據關節來移動，所以我們也是根據每一個關節來讓整個模型移動，不過因為網上的模型並沒有區分手肘或是大小腿，所以我們利用好幾條直線來將整個身體切成14個部分，分成「頭」「身體」「左右上下手臂」「左右手腕」「左右大小腿」「左右腳掌」。

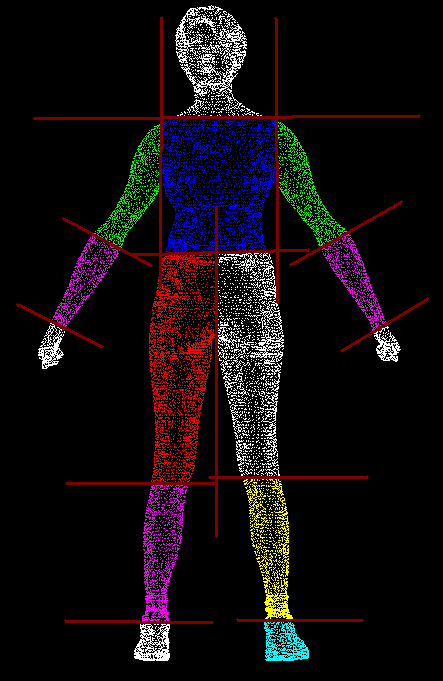
    6. 運算關節點位置：我們利用分好的部分資訊來運算關節點。比如說我們要算左手肘這個關節點，那我們將左上手臂最靠近手肘的10個點，跟左下手臂最靠近手肘的10個點來算出關節點位置。那怎麼知道最靠近手肘是哪些點 ? 我們是利用Y軸的方向來取得靠近手肘的關節點。
    7. 初始化模型位置：因為影片中的第一張frame的初始位置並不是跟模型的初始位置一樣，因此我們利用Quaternion and Rotation[3]來將模型的位置調成跟影片的位置一樣。

  • 模型運動

    1. 分析資料：我們先試著把得到的3-D偵測資料顯示在螢幕上，當然也是用OpenGL來完成，而且我們把每兩個關節點連成一條線來看它的移動情形。結果發現，得到的關節點資料所構成的人形，跟我們抓到的的模型，大小上有一定的差距，這個問題在旋轉方面是不講成問題，但是在平移方面卻有可能有一定的影響力。
    2. 旋轉關節點：我們已經將各個關節點都已經求出來了，所以我們現在依照偵測資料去運算要旋轉多少或是平移多少。
      1. 假設現在要旋轉 a、b兩個關節點，我們得到資料為
        T0：a0(Px1, Py2, Pz1)，b0(Px2, Py2, Pz2)
        T1：a1(Nx1, Ny2, Nz1)，b1(Nx2, Ny2, Nz2)
      2. V0 = a0 - b0, V1 = a1 - b1
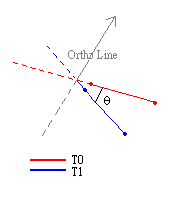
      3. 用V0、V1這兩個向量去構成一個平面並算出其法向量Ortho[1]，用Ortho去當作旋轉軸使得V0旋轉到V1。
      4. 用V0、V1那兩個向量算出其夾角θ[2]。
      5. 套用在模型上，根據Ortho、θ以及T0時的模型關節點位置，用Quaternion and Rotation[3]去旋轉模型的關節點。
    3. 非關節點移動：在3-D空間中要旋轉每一個點，必需要有一個旋轉點，一個旋轉軸，以及旋轉角度。因此在旋轉所有點的時候，每一個點必需相對應有一個旋轉點，因此我們抓每一個部位的靠近頭的關節點當作旋轉點，例如上手臂就抓肩膀，大腿就抓骨盆，小腿就抓膝蓋......等等。
             
    4. 貼三角片：我們之前所著重的都是點的移動，因為如果點的移動是正常的，那麼三角片也不會失真，不過要注意的就是在背後的三角片不能顯示，這個問題由OpenGL就可以解決了。

3. Flow diagram

4. Experimental Results

   ben02 影片模擬

   ben03 影片模擬

從研究結果可以看出來，模型並沒有很精確的跟著影片運動。我們發現了兩種可能：

  1. 可能是因為偵測資料的些許誤差，而造成模型運動時的誤差。
  2. 可能是因為Quaternion and rotation的旋轉方式，再加上是因為浮點數的運算，所以造成數字上的誤差，而因為時間愈長，所以累積的誤差愈多，造成運動的不正確。

5. Difficulties

有問是的是旋轉那一方面，一開始的做法是投影在x-y平面上，然後去做旋轉，再投影於y-z平面上，做第二 次旋轉，即是使用x軸以及z軸去當做旋轉軸。用此方法來達成我們在3D空間中的旋轉。
後來實際去實作出來的結果並不是我們所期望的。後來我們參考已畢業學長的paper，發現到可以運用Quaternion and Rotations 去達成我們所需的3D空間中旋轉。去實作出來的效果出乎意料的好，不過，當我們把全身都畫出來的時候 ，發現有時候腳或手會有不正常的運動，發現最有可能的兩點是：
  1. 得到的"火柴人"的比例跟模型的比例相差太大，導致移動的角度過大。
  2. 因為是用2D畫面來偵測3D空間的運動，所以對於z軸的偵測會有誤差，而這個誤差可能會因為時間愈長，導致誤差累積，所以誤差愈大。
我們將偵測出來的資料，先經過smooth，然後再去做旋轉。一些本來有的問題，都大幅減少，雖然沒辦法完全解決，不過至少看起來就比較正常了。

6. Future work

  1. 手跟腳都會因為旋轉之後，發生類似抽慉的現象。
  2. 模型還未貼Texture。
  3. 關節周圍的點，會因為彎曲而造成「收縮」以及「拉長」，不能只是依照旋轉而去動關節附近的點。
  4. 還不能Real Time運動，因所需計算量過於龐大。

7. Appendix

  1. Ortho：Orthogonal Line = V1 cross V2
  2. θin 3-D：cosθ= V1 dot V2 / |V1|*|V2|
  3. Quaternion and Rotation
    1. To rotate a 3D unit vector v around an arbitrary axis u with 2θdegrees, we first define quaternion vector q for this rotation operation as follows : q = cos(θ) + u*sin(θ)
    2. The above rotation operation on a vector v is given as follows :
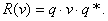
    3. V is the 4-dimensional quaternion representation of 3D unit vector v, given by v = (0, v), q* is the conjugate of q, given by
      q* = cos(θ) - u*sin(θ)

8. References

  1. Visual C++ 6 視窗程式設計經典 林俊杰
  2. OpenGL 1.1 Reference
  3. Computer Graphics (Comp236) at University of North Carolina, U.S.A
  4. 柯毅暉, 清華大學碩士論文, "3D model-based human tracking in monocular image sequences".